Lenny Conundrum 188

[AySz88]

No trig necessary, by the way, if you look up the formula for the radius of a circle that ci--*bonk!* Ugggh....what was I saying?

[ArwenEarendil]

Dear Tuum hodie vincebo, Congratulations! You have guessed correctly in the Lenny Conundrum game (round 188). You have won 685 NP! Yours Sincerely, The Neopets Team!

Cool.

In my opinion, this is about 10th grade level math (if you did it this way). So.. how I did it. The trigonometry way.

Rename the islands with variables. In this case, I used A, B and C.
Set:
a = 240 km
b = 330 km
c = 270 km



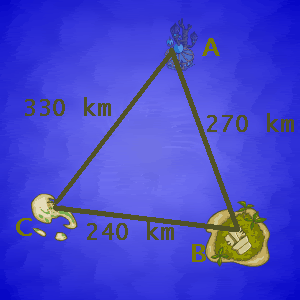
We need to find the area of the triangle with the formula for area.

Area = (ab*sin C)/2

Since we only have 3 sides and no angle, we use the Law of Cosines to find an angle.
We are trying to find the angle measure of C, so the Law of Cosines in this case is

c^2 = a^2 + b^2 - 2ab cos C

Plug in the values and solve for C:

270^2 = 240^2 + 330^2 - 2(240)(330)(cos C)
72900 = 57600 + 108900 - (158400)(cos C)
72900 = 166500 - (158400)(cos C)
-93600 = -(158400)(cos C)
.5909090909 = cos C
C = cos^-1 (.5909090909)
C = 53.77845338

REMEMBER: Don't round until you get the final answer!

So now we have angle C. Let's find the area of the triangle now.

Area = (ab*sin C)/2
Area = ((240)(330)(sin 53.77845338))/2
Area = (63893.66166)/2
Area = 31946.83083

Now. This is where I needed the help of Google. I simply searched for the string "largest circle in triangle" and came up with THIS wikipedia page:Wikipedia - Incircles

HOPING that this was right... after reading through the article, you find this:

"The radii of the in- and excircles are closely related to the area of the triangle. If S is the triangle's area and its sides are a, b and c, then the radius of the incircle (also known as the inradius) is 2S/(a+b+c)), the excircle at side a has radius 2S/(-a+b+c)), the excircle at side b has radius 2S/(a-b+c)) and the excircle at side c has radius 2S/(a+b-c))."

Since the circle is inside of the triangle, we're interested in the incircle formula. The formula for the radius of the largest possible incircle is 2S/(a+b+c) when S is the area of the triangle.

Input the values and solve:

r = (2S)/(a+b+c)
r = (2(31946.83083))/(330+270+240)
r = 63893.66166/840
r = 76.063883293

To find the area of a circle, we use the forumla Area = πr^2. So find the area.

Area = π(76.063883293)^2
Area = π(5785.714286)
Area = 18176.3575

TNT asked for the answer to the nearest hundred with no units, so we round it to 18200.

Final answer: 18200

If you see any errors in this post, feel free to PM me.

[Siouxper]

Congrats all, I rushed way too fast, and although my digits added up to 11 (the magic number between 8 and 12) I got it wrong. I never really thought about incircles, or the slant between the two sides going upwards. Guess I thought it was a square or something.

[Jerch]

Instead finding the incircle formula (on web) though, I had let the radius of the circle be r km.

Since the three sides of the triangle are tangents to the circle (the circle touches the sides), each side would be perpendicular to a radius. Thus, the area of the huge triangle can be broken down into 3 smaller ones.

ie.
(240r)/2 + (270r/2) + (330r/2) = Area

which IS the formula anyway.

[unr4veled]

I used this site: http://mathforum.org/library/drmath/view/55060.html

and the formula at the bottom of the answer...

and seem to remember getting the right answer.

But apparently i didn't.


That's why i think there should be a way to check and see what answer you submitted, just in case you forgot.

[pipsqueeek]

We need to find the area of the triangle with the formula for area.

Area = (ab*sin C)/2

Since we only have 3 sides and no angle, we use the Law of Cosines to find an angle.

Or you could use heron's formula. (the square root of(s(s-a)(s-b)(s-c), where s is the semi-perimiter and a,b, and c are sides(if I'm remembering it right off the top of my head)). Much easier if you, er, kinda skipped precalc and thus suck at trig.

[AySz88]

And, of course, I did the circle that *circumscribes* the triangle (i.e I put the triangle inside the circle, not the circle inside the triangle). Wrong way around. And I kept re-reading the problem the wrong way around too, and it only flipped the right way when I saw the picture in the new LC. Sorry for the false hint.