Quote:
Dear Tuum hodie vincebo, Congratulations! You have guessed correctly in the Lenny Conundrum game (round 188). You have won 685 NP! Yours Sincerely, The Neopets Team!
Cool.

In my opinion, this is about 10th grade level math (if you did it this way). So.. how I did it. The trigonometry way.
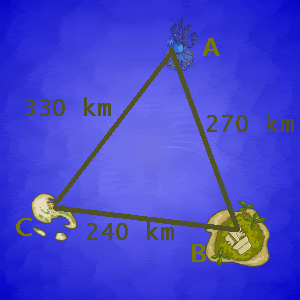
Rename the islands with variables. In this case, I used A, B and C.
Set:
a = 240 km
b = 330 km
c = 270 km
We need to find the area of the triangle with the formula for area.
Area = (ab*sin C)/2
Since we only have 3 sides and no angle, we use the Law of Cosines to find an angle.
We are trying to find the angle measure of C, so the Law of Cosines in this case is
c^2 = a^2 + b^2 - 2ab cos C
Plug in the values and solve for C:
270^2 = 240^2 + 330^2 - 2(240)(330)(cos C)
72900 = 57600 + 108900 - (158400)(cos C)
72900 = 166500 - (158400)(cos C)
-93600 = -(158400)(cos C)
.5909090909 = cos C
C = cos^-1 (.5909090909)
C = 53.77845338
REMEMBER: Don't round until you get the final answer!
So now we have angle C. Let's find the area of the triangle now.
Area = (ab*sin C)/2
Area = ((240)(330)(sin 53.77845338))/2
Area = (63893.66166)/2
Area = 31946.83083
Now. This is where I needed the help of Google. I simply searched for the string "largest circle in triangle" and came up with THIS wikipedia page:
Wikipedia - IncirclesHOPING that this was right... after reading through the article, you find this:
Quote:
"The radii of the in- and excircles are closely related to the area of the triangle. If S is the triangle's area and its sides are a, b and c, then the radius of the incircle (also known as the inradius) is 2S/(a+b+c)), the excircle at side a has radius 2S/(-a+b+c)), the excircle at side b has radius 2S/(a-b+c)) and the excircle at side c has radius 2S/(a+b-c))."
Since the circle is inside of the triangle, we're interested in the incircle formula. The formula for the radius of the largest possible incircle is 2S/(a+b+c) when S is the area of the triangle.
Input the values and solve:
r = (2S)/(a+b+c)
r = (2(31946.83083))/(330+270+240)
r = 63893.66166/840
r = 76.063883293
To find the area of a circle, we use the forumla Area = πr^2. So find the area.
Area = π(76.063883293)^2
Area = π(5785.714286)
Area = 18176.3575
TNT asked for the answer to the nearest hundred with no units, so we round it to 18200.
Final answer: 18200
If you see any errors in this post, feel free to PM me.




