Lenny Conundrum 189

Jerch · **Posts:** 329 **Joined:** Sun Sep 25, 2005 6:19 am

Quote:

While the Maraqua Circle from last week's Lenny Conundrum is well known in pirate lore, the legend of the Mystery Island Triangle is less well known. In the Mystery Island Triangle, it is rumoured that scurvy and seasickness are slightly more likely to occur. And the barnacles! Oh, the barnacles!

Anyway, the area of the Mystery Island Triangle is bounded on one side by the Maraquan Circle and on the other two sides by the lines connecting Mystery Island with Maraqua and Krawk Island.

What is the area of the Mystery Island Triangle? Please round up to the nearest 25 square kilometres, and please only submit a number! (For example, if the answer is 5156 square kilometres, only submit the number "5175".)

more complicated than last time's (though technically easier), but easy nonetheless...I keep getting the feeling that I've overcomplicated things...

Used:
Radius
A certain angle
A pair of congruent triangles
area

apranum · **Posts:** 749 **Joined:** Mon May 31, 2004 9:14 am

I hate the roundings, I got 1799 which should be 1800, the answer was 1825

Jerch · **Posts:** 329 **Joined:** Sun Sep 25, 2005 6:19 am

What I had done (err...sorry for the lack of extra graphics...):

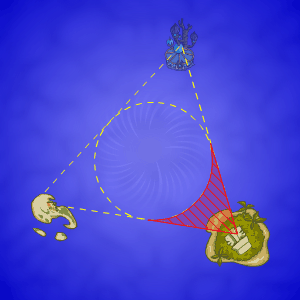
Let
M be the Mystery Island.
C be the centre of the circle. [ie the incentre of the large triangle]
K be the pt where the circle meets the line between M and Krawk Island
W be the pt where the circle meets the line between M and Maraqua

i)

congruent triangles:

CK = CW
(they are radii of the same circle)

angle CKM = angle CWM = 90 deg
(tangents...)

MC = MC
(obviously =.=)

Thus, we get triangle CKM congruent to triangle CWM
(a right angle, the hypotenuse, and a side/leg)

From this, we get:

area of CKM = area of CWM
i.e. area of CWMK = 2*(area of CKM)

angle CMK = angle CMW
i.e. angle KMW = 2*(angle CMK)

ii)

A certain angle: (or well...angles)

Using the data given in the previous LC:
By cosine law,
angle KMW = 80.406... deg

2*(angle CMK) = 80.406... deg (by (i))
angle CMK = 40.203... deg

also,
sum of interior angles of CWKM = 360 deg
angle WCK = (360 - 90 - 90 - 80.406) deg
angle WCK = 99.594... deg

iii)

radius:

From the previous LC,
radius = 76.064... km,
which includes CK.

Also remember that
angle CKM = 90 deg

Thus, by the definition of tangent,
CK / KM = tan(angle CMK) (by (ii))
KM = 90.000... km

iv)

area:

area of CKM = CK * KM /2
2*(area of CKM) = CK * KM
area of CWMK = CK * KM = 6846... sqkm

area of circle = pi * (radius)^2 = 18176... sqkm

area of sector CWK = (area of circle) * (angle WCK)/(360 deg),
which is 5028... sqkm

req. area = (area of CWMK) - (area of sector CWK),
which is 1818... sqkm.

Hence, rounding up, we would get 1825 sqkm.

bonsgun · **Posted:** Thu Nov 02, 2006 1:31 pm

wow, you'd made the calculation easy. i calculated it like about 45mins before getting the answer, but my answer is 1817.

Jerch · **Posts:** 329 **Joined:** Sun Sep 25, 2005 6:19 am

bonsgun wrote:

wow, you'd made the calculation easy. i calculated it like about 45mins before getting the answer, but my answer is 1817.

now that I think of it, yeah, my answer was also 1817 (1817.256717... to be exact) in the original calculation

thus the reason why I shouldn't have rounded off before the final answer like I've done in the 'proof'.... but well...I got lazy...><

the problem's actually at the last step (or at least, it seems to be):
6845.75.. is rounded to 6846.
5028.49.. is rounded to 5028.

6845.75... - 5028.49... = 1817.26...
6846 - 5028 = 1818

ie, the error

Pink Poogle Toy Forum

Lenny Conundrum 189

Who is online